两层神经网络
import sys, os
import numpy as np
# sigmoid 函数:把任意数值压缩到 0-1 之间(用于隐藏层)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_grad(x):
"""sigmoid 函数的导数:用于反向传播时计算梯度
数学形式:d(sigmoid)/dx = sigmoid(x) * (1 - sigmoid(x))
"""
return (1.0 - sigmoid(x)) * sigmoid(x)
# softmax 函数:把任意数值转换成 0-1 之间的概率(用于输出层)
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # 减去最大值,防止数值溢出(计算稳定性技巧)
return np.exp(x) / np.sum(np.exp(x)) # 指数归一化成概率
def cross_entropy_error(y, t):
"""交叉熵损失函数:衡量模型预测和真实标签的差距
参数
-----
y : numpy.ndarray
模型预测的概率分布(由 softmax 输出)
t : numpy.ndarray
真实标签(独热编码或类别索引)
返回
----
float
交叉熵损失(数值越小表示预测越准确)
"""
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 如果标签是独热编码(如 [0, 1, 0]),转换成类别索引(如 1)
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
# 计算平均的交叉熵(加个很小的值 1e-7 防止取对数时出现负无穷)
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
def numerical_gradient(f, x):
"""数值梯度计算函数:用有限差分法近似计算函数 f 对 x 的梯度
原理:梯度 ≈ (f(x+h) - f(x-h)) / (2*h),其中 h 是一个很小的数
参数
-----
f : callable
目标函数(接受 x 返回标量)
x : numpy.ndarray
输入变量(可以是向量或矩阵)
返回
----
grad : numpy.ndarray
梯度,与 x 形状相同
"""
h = 1e-4 # 很小的步长(0.0001),用来近似导数
grad = np.zeros_like(x) # 初始化梯度数组
# 遍历 x 的每个元素
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index # 获取当前元素的索引
tmp_val = x[idx] # 保存原始值
# 计算 f(x+h):第 idx 个元素增加 h
x[idx] = float(tmp_val) + h
fxh1 = f(x)
# 计算 f(x-h):第 idx 个元素减少 h
x[idx] = tmp_val - h
fxh2 = f(x)
# 用中心差分公式计算梯度(偏导数)
grad[idx] = (fxh1 - fxh2) / (2*h)
# 恢复原始值,准备计算下一个元素
x[idx] = tmp_val
it.iternext()
return grad
class TwoLayerNet:
"""两层神经网络类:输入 -> 隐藏层 -> 输出层
这是一个简单的多层感知机(MLP),用 sigmoid 激活隐藏层,softmax 激活输出层。
"""
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
"""初始化网络的权重和偏置(用随机数填充)。
参数
-----
input_size : 输入节点个数
hidden_size : 隐藏层节点个数
output_size : 输出节点个数
weight_init_std : 权重初始化的随机数大小(较小的数有利于训练)
"""
# 创建网络参数字典,存放所有权重和偏置
self.params = {}
# 第一层(输入到隐藏层)的权重和偏置
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
# 第二层(隐藏层到输出层)的权重和偏置
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
"""前向传播:输入数据通过网络得到预测结果。
计算过程:输入 -> (W1, b1) -> sigmoid -> (W2, b2) -> softmax -> 输出概率
"""
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
# 第一层:输入 dot 权重 + 偏置,然后通过 sigmoid 激活
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
# 第二层:隐藏层输出 dot 权重 + 偏置,然后通过 softmax 激活得到概率
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
def loss(self, x, t):
"""计算损失函数值:衡量网络预测与真实标签的误差
参数
-----
x : numpy.ndarray
输入数据,形状 (样本数, 输入维度)
t : numpy.ndarray
真实标签,形状 (样本数, 输出维度) 或 (样本数,)
返回
----
float
交叉熵损失值
"""
y = self.predict(x) # 前向传播得到预测结果
return cross_entropy_error(y, t) # 计算损失
def accuracy(self, x, t):
"""计算网络的准确率:预测正确的样本数量占比
参数
-----
x : numpy.ndarray
输入数据,形状 (样本数, 输入维度)
t : numpy.ndarray
真实标签,形状 (样本数, 输出维度)(通常是独热编码)
返回
----
float
准确率,范围 0-1(0 = 全错,1 = 全对)
"""
y = self.predict(x) # 前向传播得到预测概率
y = np.argmax(y, axis=1) # 选择概率最大的类别作为预测结果
t = np.argmax(t, axis=1) # 从独热编码转换为类别索引
# 比较预测和真实标签,计算相等的数量占比
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
"""用数值微分法计算所有参数的梯度(速度慢,但易于理解和验证)
参数
-----
x : numpy.ndarray
输入数据,形状 (样本数, 输入维度)
t : numpy.ndarray
真实标签,形状 (样本数, 输出维度)
返回
----
grads : dict
梯度字典,包含 'W1', 'b1', 'W2', 'b2' 四个梯度值
"""
# 定义一个关于权重 W 的损失函数(用于数值微分)
loss_W = lambda W: self.loss(x, t)
# 计算每个参数的梯度
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
"""用反向传播算法计算所有参数的梯度(比数值微分快得多)
这是深度学习中最常用的梯度计算方法,通过链式法则从输出层反向计算每层的梯度。
参数
-----
x : numpy.ndarray
输入数据,形状 (样本数, 输入维度)
t : numpy.ndarray
真实标签,形状 (样本数, 输出维度)
返回
----
grads : dict
梯度字典,包含 'W1', 'b1', 'W2', 'b2' 四个梯度值
"""
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0] # 批次中样本的个数
# ========== 前向传播:计算网络输出 ==========
a1 = np.dot(x, W1) + b1 # 第一层的线性变换
z1 = sigmoid(a1) # 第一层的激活函数
a2 = np.dot(z1, W2) + b2 # 第二层的线性变换
y = softmax(a2) # 第二层的激活函数(输出概率)
# ========== 反向传播:从输出层开始反向计算梯度 ==========
# 第二层的梯度:(预测概率 - 真实标签) / 样本数(这来自交叉熵+ softmax 的求导)
dy = (y - t) / batch_num
# 计算第二层参数的梯度
grads['W2'] = np.dot(z1.T, dy) # 隐藏层激活的转置 dot 输出误差
grads['b2'] = np.sum(dy, axis=0) # 沿样本维度求和得到偏置梯度
# 第一层的梯度:反向传播误差
da1 = np.dot(dy, W2.T) # 误差通过权重 W2 反向传播
dz1 = sigmoid_grad(a1) * da1 # 乘以 sigmoid 导数(链式法则)
# 计算第一层参数的梯度
grads['W1'] = np.dot(x.T, dz1) # 输入的转置 dot 第一层误差
grads['b1'] = np.sum(dz1, axis=0) # 沿样本维度求和得到偏置梯度
return grads
函数解释
| 函数名 | 功能描述 | 用途 |
|---|---|---|
sigmoid(x) |
将任意数值压缩到 0-1 之间 | 隐藏层激活函数 |
sigmoid_grad(x) |
计算 sigmoid 的导数值 | 反向传播计算梯度 |
softmax(x) |
将任意数值转换为 0-1 的概率分布 | 输出层激活函数 |
cross_entropy_error(y, t) |
计算模型预测与真实标签的误差 | 损失函数 |
numerical_gradient(f, x) |
使用有限差分法计算函数梯度 | 验证反向传播算法正确性 |
TwoLayerNet.__init__() |
初始化网络的权重和偏置 | 网络参数初始化 |
TwoLayerNet.predict(x) |
前向传播计算网络预测值 | 预测输出 |
TwoLayerNet.loss(x, t) |
计算交叉熵损失函数值 | 评估训练效果 |
TwoLayerNet.accuracy(x, t) |
计算分类准确率 | 评估模型性能 |
TwoLayerNet.numerical_gradient(x, t) |
用数值微分法计算梯度 | 梯度验证用 |
TwoLayerNet.gradient(x, t) |
用反向传播算法计算梯度 | 训练网络用(推荐) |
训练流程
前向传播 → 计算损失 → 反向传播 → 更新参数 → 循环
梯度计算方法对比
| 梯度计算方法 | 计算速度 | 易用性 | 应用场景 |
|---|---|---|---|
| 数值微分 | 🔴 很慢 | 🟢 易于理解 | 验证和学习用 |
| 反向传播 | 🟢 很快 | 🟡 需要数学基础 | 实际训练用 |
MNIST 数据训练
import numpy as np
from mnist_demo import load_mnist
from two_layer import TwoLayerNet
# 加载 MNIST 手写数字数据集
# normalize=True:像素值缩放到 0-1(便于神经网络处理)
# flatten=True:把 28x28 的图片展平成 784 维向量
# one_hot_label=True:标签转换成独热编码(例如 5 变成 [0,0,0,0,0,1,0,0,0,0])
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=True)
train_loss_list = [] # 存储每次迭代的损失值,用于画图观察训练过程
# ========== 训练超参数设置 ==========
# 这些是神经网络训练时需要手动调整的参数
iters_num = 10000 # 总共训练多少步(每步处理一个小批量数据)
train_size = x_train.shape[0] # 训练集中有多少张图片
batch_size = 100 # 每次训练用多少张图片(100 张为一个批次)
learning_rate = 0.1 # 学习率:控制每次参数更新的幅度(数值越大学习越快,但可能跳过最优值)
# 初始化神经网络:784 个输入 -> 100 个隐藏层节点 -> 10 个输出(0-9 十个数字)
network = TwoLayerNet(input_size=784, hidden_size=100, output_size=10)
# ========== 开始训练循环 ==========
for i in range(iters_num):
# 从训练集中随机抽取 batch_size 张图片(小批量随机抽样,这样训练更稳定)
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask] # 抽取的图片数据
t_batch = t_train[batch_mask] # 抽取的图片标签
# 计算梯度:梯度告诉我们参数应该往哪个方向调整才能减小损失
grad = network.numerical_gradient(x_batch, t_batch)
# grad = network.gradient(x_batch, t_batch) # 可以用更快的反向传播计算梯度
# 参数更新:沿着梯度的反方向(下降方向)调整参数
# 新参数 = 旧参数 - 学习率 × 梯度
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 计算当前小批量的损失值(衡量预测有多错误)
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss) # 记录这一步的损失值
# 每 1000 步打印一次进度和损失值
if i % 1000 == 0:
print(f"训练进度: 第 {i} 步,当前损失值: {loss:.4f}")
# ========== 训练完成,绘制损失函数曲线 ==========
import matplotlib.pyplot as plt
# 创建图表
plt.figure(figsize=(12, 6))
# 绘制损失函数值推移曲线
plt.plot(train_loss_list, linewidth=0.5)
# 设置图表标题和标签
plt.title("训练过程中的损失函数值变化", fontsize=14, fontweight='bold')
plt.xlabel("迭代次数(每次处理 100 张图片)", fontsize=12)
plt.ylabel("损失函数值(交叉熵)", fontsize=12)
# 添加网格线,便于观察
plt.grid(True, alpha=0.3)
# 添加文本说明
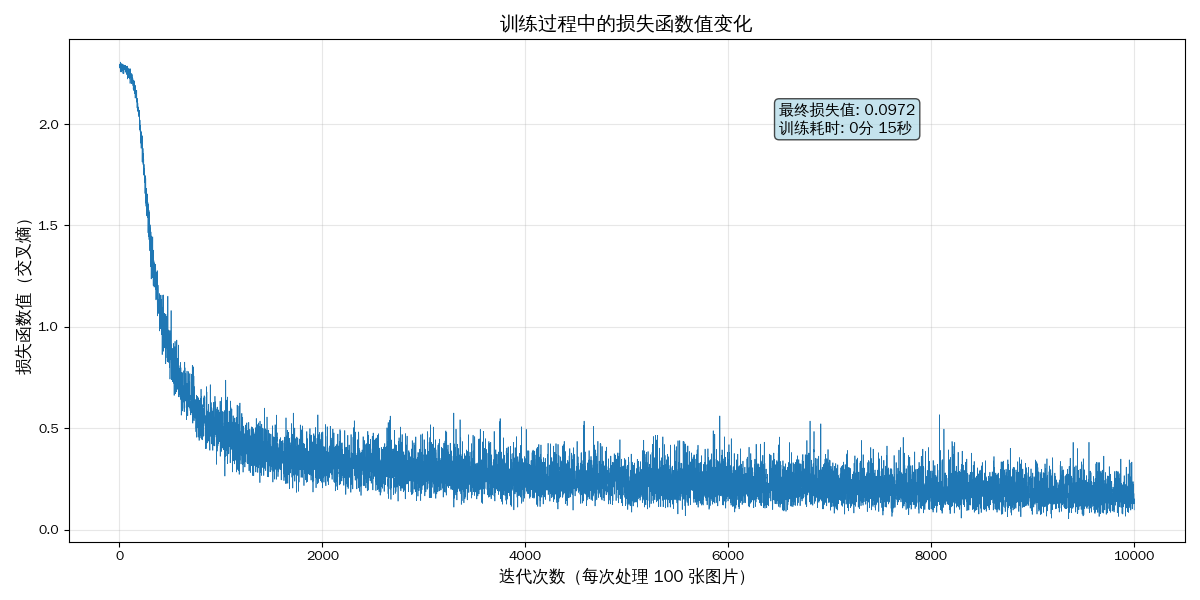
final_loss = train_loss_list[-1]
plt.text(len(train_loss_list) * 0.7, max(train_loss_list) * 0.9,
f'最终损失值: {final_loss:.4f}',
fontsize=11, bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5))
# 紧密布局(防止标签被切割)
plt.tight_layout()
# 显示图表
plt.show()
# 打印训练统计信息
print(f"\n========== 训练完成 ==========")
print(f"总迭代次数: {iters_num}")
print(f"初始损失值: {train_loss_list[0]:.4f}")
print(f"最终损失值: {train_loss_list[-1]:.4f}")
print(f"损失下降幅度: {(train_loss_list[0] - train_loss_list[-1]):.4f}")
默认是使用 CPU 进行训练的
- NumPy 只在 CPU 上运行
- 不支持 GPU 加速
- 所有矩阵运算(前向、梯度、更新)都是 CPU 完成
总结
| 问题 | 答案 |
|---|---|
| 这段代码默认GPU训练吗 | ❌ 不是 |
| 现在跑在哪 | CPU |
| 为什么 | 用的是 NumPy |
| 想用GPU怎么办 | PyTorch / TensorFlow / CuPy |
| 最大性能瓶颈在哪 | numerical_gradient(数值求导) |
训练时间对比
AMD Ryzen 9 5950X 16-Core Processor
| 方式 | 原理 | 训练时间 |
|---|---|---|
| numerical_gradient(你现在用的) | 数值微分(逐参数扰动) | 8~30 小时 |
| 反向传播 gradient | 链式法则一次算完所有梯度 | 1~3 分钟 |
改成反向传播训练
# 计算梯度:梯度告诉我们参数应该往哪个方向调整才能减小损失
# grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch) # 可以用更快的反向传播计算梯度
训练过程
第 0 步:2.2942
第 1000 步:0.5611
第 2000 步:0.4726
第 3000 步:0.3393
第 4000 步:0.2660
第 5000 步:0.2507
第 6000 步:0.2323
第 7000 步:0.3340
第 8000 步:0.2121
第 9000 步:0.1369
最终:0.2750
模型性能
- 初始损失值:2.2864(未训练状态)
- 最终损失值:0.0972(训练后)
- 损失下降幅度:95.7%(从 2.2864 降至 0.0972)
训练效率
- 总迭代次数:10,000 步
- 总训练耗时:15.75 秒
- 平均每步耗时:1.57 毫秒
数据集与网络配置
- MNIST 手写数字数据集(60,000 张训练图片)
- 网络结构:784 → 100 → 10(两层神经网络)
- 批处理大小:每批 100 张图片
- 学习率:0.1
预测准确率
测试集准确率:92.07%
人工智能效率时间线
| 时间 | 事件/突破 | 核心效率革命 | 对训练效率影响 |
|---|---|---|---|
| 1943-1958 | 神经网络雏形(McCulloch-Pitts、感知机) | 简单线性计算 | 可以做简单分类,但仅能处理小规模问题 |
| 1960s-1970s | 感知机发展 & XOR问题提出 | 算法限制显现 | 训练深层网络不可行,效率极低 |
| 1986 | 反向传播算法(Rumelhart 等) | 链式法则自动求梯度 | 数值微分 → 反向传播,训练速度提高数百倍 |
| 1990s | 小型神经网络 & CPU训练 | 软件优化 + mini-batch | 训练 MNIST 等小数据集可在分钟~小时级完成 |
| 2006 | 深度信念网络(Hinton) | 无监督预训练 | 更深网络可训练,减少梯度消失问题 |
| 2010 | GPU用于深度学习(CUDNN + CUDA) | 并行矩阵计算 | MNIST/Imagenet训练速度从小时 → 几分钟/小时 |
| 2012 | AlexNet赢ImageNet | GPU + ReLU + dropout | 图像识别性能暴增,深度学习真正爆发 |
| 2015 | 高效框架(TensorFlow, PyTorch) | 自动求导 + GPU优化 | 训练速度快,开发效率提高,普通研究者也能训练模型 |
| 2020 | 大语言模型(GPT, BERT) | 超大规模并行 + 分布式训练 | 参数量从亿 → 千亿级,训练耗时依旧可控(秒 → 天) |
| 2023+ | 垂直/低成本大模型 & GPU/TPU 云端 | 算法 + 硬件协同 | 个人和小团队也能训练行业模型,训练效率达到新高 |
查看本机GPU
$ nvidia-smi
Thu Feb 12 17:12:08 2026
+-----------------------------------------------------------------------------------------+
| NVIDIA-SMI 580.126.09 Driver Version: 580.126.09 CUDA Version: 13.0 |
+-----------------------------------------+------------------------+----------------------+
| GPU Name Persistence-M | Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap | Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|=========================================+========================+======================|
| 0 NVIDIA GeForce RTX 3070 Off | 00000000:07:00.0 On | N/A |
| 30% 41C P2 53W / 180W | 2555MiB / 8192MiB | 2% Default |
| | | N/A |
+-----------------------------------------+------------------------+----------------------+
+-----------------------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=========================================================================================|
| 0 N/A N/A 2078 G /usr/lib/xorg/Xorg 1239MiB |
| 0 N/A N/A 2213 G /usr/bin/gnome-shell 227MiB |
| 0 N/A N/A 2482 G clash-nyanpasu 3MiB |
| 0 N/A N/A 20456 G ...rack-uuid=3190708988185955192 201MiB |
| 0 N/A N/A 274485 G /usr/share/code/code 276MiB |
| 0 N/A N/A 290452 G ...x/android-studio/jbr/bin/java 21MiB |
| 0 N/A N/A 1796518 C /bin/python3 506MiB |
+-----------------------------------------------------------------------------------------+
第一部分
- NVIDIA-SMI 580.126.09 → NVIDIA 系统管理接口(S.M.I.)版本
- Driver Version: 580.126.09 → 当前 NVIDIA 显卡驱动版本
- CUDA Version: 13.0 → 当前驱动支持的 CUDA 版本
第二部分
- GPU Name → 显卡型号:RTX 3070
- Persistence-M → 持久模式(控制 GPU 驱动是否持续保留内存/上下文)
- Bus-Id → PCIe 总线位置
- Disp.A → 是否用于显示输出(Yes/No)
- Volatile Uncorr. ECC → 错误校正码状态(N/A 表示无 ECC)
- Fan → 风扇转速(%)
- Temp → GPU 温度(℃)
- Perf → 当前性能状态(P0 最快,P2 省电)
- Pwr:Usage/Cap → 当前功耗 / 最大功耗(W)
- Memory-Usage → 显存占用 / 总显存(MB)
- GPU-Util → GPU 利用率(%)
- Compute M. → 当前计算模式
第三部分
- GPU → 使用该显卡编号
- GI / CI → GPU Instance / Compute Instance(多实例模式,N/A 表示未启用)
- PID → 占用 GPU 的进程 ID
- Type → C = 计算 (Compute),G = 图形 (Graphics)
- Process name → 占用 GPU 的程序
- GPU Memory Usage → 占用显存大小
Pytorch GPU 版本安装

$ pip3 install torch torchvision --index-url https://download.pytorch.org/whl/cu130
Defaulting to user installation because normal site-packages is not writeable
Looking in indexes: https://download.pytorch.org/whl/cu130
Requirement already satisfied: torch in /home/lxg/.local/lib/python3.10/site-packages (2.6.0+cu124)
Requirement already satisfied: torchvision in /home/lxg/.local/lib/python3.10/site-packages (0.21.0+cu124)
Requirement already satisfied: nvidia-cudnn-cu12==9.1.0.70 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (9.1.0.70)
Requirement already satisfied: nvidia-nvjitlink-cu12==12.4.127 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (12.4.127)
Requirement already satisfied: sympy==1.13.1 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (1.13.1)
Requirement already satisfied: triton==3.2.0 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (3.2.0)
Requirement already satisfied: nvidia-cublas-cu12==12.4.5.8 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (12.4.5.8)
Requirement already satisfied: typing-extensions>=4.10.0 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (4.15.0)
Requirement already satisfied: nvidia-cufft-cu12==11.2.1.3 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (11.2.1.3)
Requirement already satisfied: nvidia-cuda-runtime-cu12==12.4.127 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (12.4.127)
Requirement already satisfied: filelock in /home/lxg/.local/lib/python3.10/site-packages (from torch) (3.20.3)
Requirement already satisfied: nvidia-cusolver-cu12==11.6.1.9 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (11.6.1.9)
Requirement already satisfied: nvidia-curand-cu12==10.3.5.147 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (10.3.5.147)
Requirement already satisfied: nvidia-cusparselt-cu12==0.6.2 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (0.6.2)
Requirement already satisfied: nvidia-nvtx-cu12==12.4.127 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (12.4.127)
Requirement already satisfied: networkx in /home/lxg/.local/lib/python3.10/site-packages (from torch) (3.3)
Requirement already satisfied: nvidia-cuda-cupti-cu12==12.4.127 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (12.4.127)
Requirement already satisfied: jinja2 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (3.1.4)
Requirement already satisfied: fsspec in /home/lxg/.local/lib/python3.10/site-packages (from torch) (2024.6.1)
Requirement already satisfied: nvidia-nccl-cu12==2.21.5 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (2.21.5)
Requirement already satisfied: nvidia-cuda-nvrtc-cu12==12.4.127 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (12.4.127)
Requirement already satisfied: nvidia-cusparse-cu12==12.3.1.170 in /home/lxg/.local/lib/python3.10/site-packages (from torch) (12.3.1.170)
Requirement already satisfied: mpmath<1.4,>=1.1.0 in /home/lxg/.local/lib/python3.10/site-packages (from sympy==1.13.1->torch) (1.3.0)
Requirement already satisfied: numpy in /home/lxg/.local/lib/python3.10/site-packages (from torchvision) (2.1.1)
Requirement already satisfied: pillow!=8.3.*,>=5.3.0 in /home/lxg/.local/lib/python3.10/site-packages (from torchvision) (10.4.0)
Requirement already satisfied: MarkupSafe>=2.0 in /home/lxg/.local/lib/python3.10/site-packages (from jinja2->torch) (2.1.5)
验证pytorch是否已经安装
import torch
x = torch.rand(5, 3)
print(x)
# tensor([[0.6462, 0.3514, 0.2290],
# [0.5519, 0.8355, 0.9929],
# [0.0225, 0.2399, 0.3644],
# [0.0654, 0.3948, 0.8368],
# [0.2206, 0.8843, 0.5664]])
改成GPU PyTorch训练
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import time # 用于记录训练耗时
from mnist_demo import load_mnist
import matplotlib.pyplot as plt
# ========== 设置 GPU 设备 ==========
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(f"使用设备: {device}")
print(f"GPU 型号: {torch.cuda.get_device_name(0) if torch.cuda.is_available() else 'CPU'}")
print()
# 加载 MNIST 手写数字数据集
# normalize=True:像素值缩放到 0-1(便于神经网络处理)
# flatten=True:把 28x28 的图片展平成 784 维向量
# one_hot_label=True:标签转换成独热编码(例如 5 变成 [0,0,0,0,0,1,0,0,0,0])
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=True)
# 转换为 PyTorch 张量并移到 GPU
x_train = torch.from_numpy(x_train).float().to(device)
t_train = torch.from_numpy(t_train).float().to(device)
x_test = torch.from_numpy(x_test).float().to(device)
t_test = torch.from_numpy(t_test).float().to(device)
train_loss_list = [] # 存储每次迭代的损失值,用于画图观察训练过程
# ========== 定义两层神经网络 ==========
class TwoLayerNetPyTorch(nn.Module):
def __init__(self, input_size=784, hidden_size=100, output_size=10):
super(TwoLayerNetPyTorch, self).__init__()
# 第一层:784 -> 100
self.fc1 = nn.Linear(input_size, hidden_size)
# 第二层:100 -> 10
self.fc2 = nn.Linear(hidden_size, output_size)
# 激活函数
self.sigmoid = nn.Sigmoid()
def forward(self, x):
# 第一层 + sigmoid 激活
x = self.sigmoid(self.fc1(x))
# 第二层 + softmax(在损失函数中做,这里直接输出)
x = self.fc2(x)
return x
# 初始化网络
network = TwoLayerNetPyTorch(input_size=784, hidden_size=100, output_size=10).to(device)
# ========== 训练超参数设置 ==========
iters_num = 10000 # 总共训练多少步
train_size = x_train.shape[0] # 训练集中有多少张图片
batch_size = 100 # 每次训练用多少张图片
learning_rate = 0.1 # 学习率
# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss() # 交叉熵损失
optimizer = optim.SGD(network.parameters(), lr=learning_rate)
# ========== 记录训练开始时间 ==========
start_time = time.time()
print("=" * 50)
print("开始在 GPU 上训练神经网络...")
print("=" * 50)
# ========== 开始训练循环 ==========
for i in range(iters_num):
# 从训练集中随机抽取 batch_size 张图片
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 前向传播
outputs = network(x_batch)
# 计算损失(t_batch 需要转换为类别索引)
# t_batch 是独热编码,需要转换为类别索引
t_batch_indices = torch.argmax(t_batch, dim=1)
loss = criterion(outputs, t_batch_indices)
# 反向传播和参数更新
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 记录损失值
train_loss_list.append(loss.item())
# 每 1000 步打印一次进度
if i % 1000 == 0:
print(f"训练进度: 第 {i} 步,当前损失值: {loss.item():.4f}")
# ========== 计算训练耗时 ==========
end_time = time.time()
elapsed_time = end_time - start_time
minutes = int(elapsed_time // 60)
seconds = int(elapsed_time % 60)
# ========== 评估模型 ==========
network.eval() # 设置为评估模式
with torch.no_grad():
# 测试集准确率
test_outputs = network(x_test)
test_preds = torch.argmax(test_outputs, dim=1)
test_labels = torch.argmax(t_test, dim=1)
test_accuracy = (test_preds == test_labels).float().mean().item()
print(f"\n测试集准确率: {test_accuracy:.4f} ({test_accuracy * 100:.2f}%)")
# ========== 设置 matplotlib 支持中文显示 ==========
plt.rcParams['font.sans-serif'] = ['SimHei', 'Noto Sans CJK SC', 'WenQuanYi Zen Hei', 'DejaVu Sans', 'Liberation Sans']
plt.rcParams['axes.unicode_minus'] = False
# ========== 绘制损失函数曲线 ==========
plt.figure(figsize=(12, 6))
# 绘制损失函数值推移曲线
plt.plot(train_loss_list, linewidth=0.5)
# 设置图表标题和标签
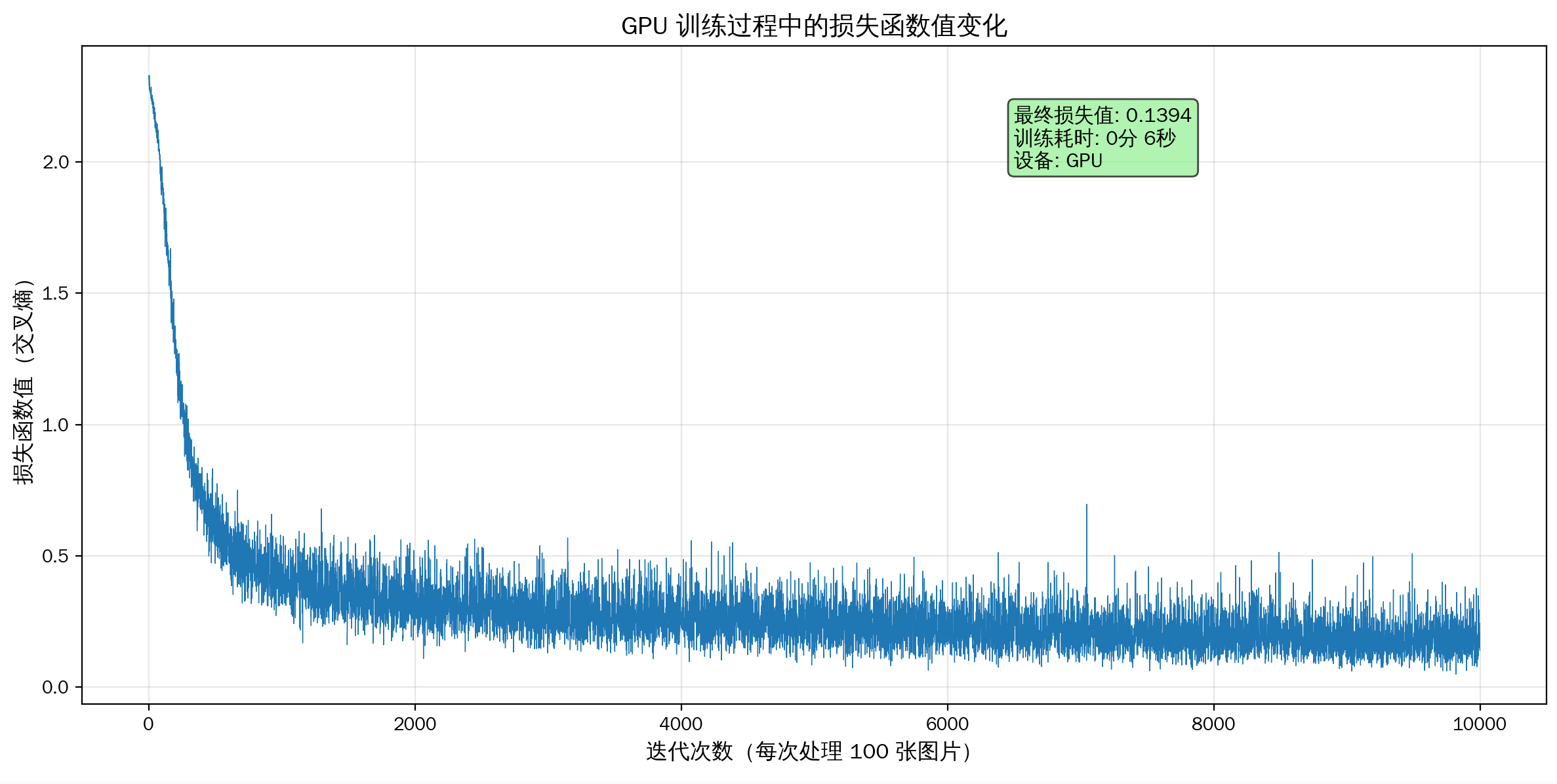
plt.title("GPU 训练过程中的损失函数值变化", fontsize=14, fontweight='bold')
plt.xlabel("迭代次数(每次处理 100 张图片)", fontsize=12)
plt.ylabel("损失函数值(交叉熵)", fontsize=12)
# 添加网格线
plt.grid(True, alpha=0.3)
# 添加文本说明
final_loss = train_loss_list[-1]
info_text = f'最终损失值: {final_loss:.4f}\n训练耗时: {minutes}分 {seconds}秒\n设备: GPU'
plt.text(len(train_loss_list) * 0.65, max(train_loss_list) * 0.85,
info_text,
fontsize=11, bbox=dict(boxstyle='round', facecolor='lightgreen', alpha=0.7))
# 紧密布局
plt.tight_layout()
# 显示图表
plt.show()
# ========== 打印训练统计信息 ==========
print(f"\n{'=' * 50}")
print(f" GPU 训练完成!")
print(f"{'=' * 50}")
print(f"总迭代次数: {iters_num}")
print(f"初始损失值: {train_loss_list[0]:.4f}")
print(f"最终损失值: {train_loss_list[-1]:.4f}")
print(f"损失下降幅度: {(train_loss_list[0] - train_loss_list[-1]):.4f}")
print(f"\n⏱️ 训练耗时: {minutes} 分 {seconds} 秒(共 {elapsed_time:.2f} 秒)")
print(f"平均每步耗时: {elapsed_time / iters_num * 1000:.2f} 毫秒")
print(f"{'=' * 50}")
Pytorch 和 CUDA 在人工智能开发中的位置
| 层级 | 作用 | 典型工具 |
|---|---|---|
| 硬件层(Compute Hardware) | 提供原始算力,矩阵运算、卷积运算等密集计算 | CPU、GPU(NVIDIA RTX)、TPU、FPGA |
| 驱动与底层加速层(Hardware Acceleration / API) | 将高层算法翻译为硬件可执行指令,实现并行计算和加速 | CUDA(NVIDIA GPU)、cuDNN、ROCm(AMD GPU)、OpenCL |
| 深度学习框架层(Framework / API) | 提供高层接口:定义网络、计算梯度、优化参数,隐藏底层复杂性 | PyTorch、TensorFlow、JAX |
开源对比
| 对比项 | PyTorch | CUDA |
|---|---|---|
| 是否开源 | ✅ 是 | ❌ 否 |
| 作用层级 | 框架层(Python API、模型定义、训练逻辑) | 驱动 + GPU 核心计算 |
| 可修改性 | 完全可以修改、优化、添加算子 | 不能修改,只能调用接口 |
| 原因 | 社区驱动、研究共享、加速生态发展 | GPU 硬件专利和商业核心,闭源保护商业利益 |
CUDA 是 NVIDIA 的核心竞争力和生态锁定工具,短期内无法复制。华为选择闭环自研生态,AMD选择开源跨平台策略,而不是造一个“属于自己大 CUDA”
| 框架 | CPU | NVIDIA GPU | AMD GPU | Google TPU |
|---|---|---|---|---|
| PyTorch | ✅ | ✅ (CUDA/cuDNN) | ✅ (ROCm) | ✅ (torch_xla) |
| TensorFlow | ✅ | ✅ (CUDA/cuDNN) | ✅ (ROCm) | ✅ (原生支持 TPU) |
Google 能做到全栈闭环,因为它从硬件、编译器到框架和云全自研,每一层都可以协同优化;而 NVIDIA、AMD 或国产 GPU 都是硬件为核心,生态、框架和云服务依赖外部资源,因此无法完全脱离第三方(如 CUDA)形成闭环
阿里如果有了自己的TPU,是否类似于google的模式了
| 层面 | Google TPU 模式 | 阿里实现条件 |
|---|---|---|
| 硬件 | TPU Matrix Core,自研 AI 加速器,高度优化矩阵计算和卷积 | 阿里需要完全自主设计的 AI 加速芯片(矩阵乘/卷积/注意力优化) |
| 编译器/驱动 | XLA:TensorFlow 运算编译成 TPU 指令,自动调度内存/矩阵 | 阿里需要类似 XLA 的 JIT 编译器,将框架运算映射到自研 TPU |
| 深度学习框架 | TensorFlow 与 TPU 完全融合,框架 API 可直接调用 TPU | 阿里需要框架(Paddle/MindSpore)原生支持 TPU API,算子高度优化 |
| 云/集群 | Google Cloud TPU + 分布式训练环境 | 阿里需要自家云(阿里云)支持 TPU 调度、分布式训练和推理 |
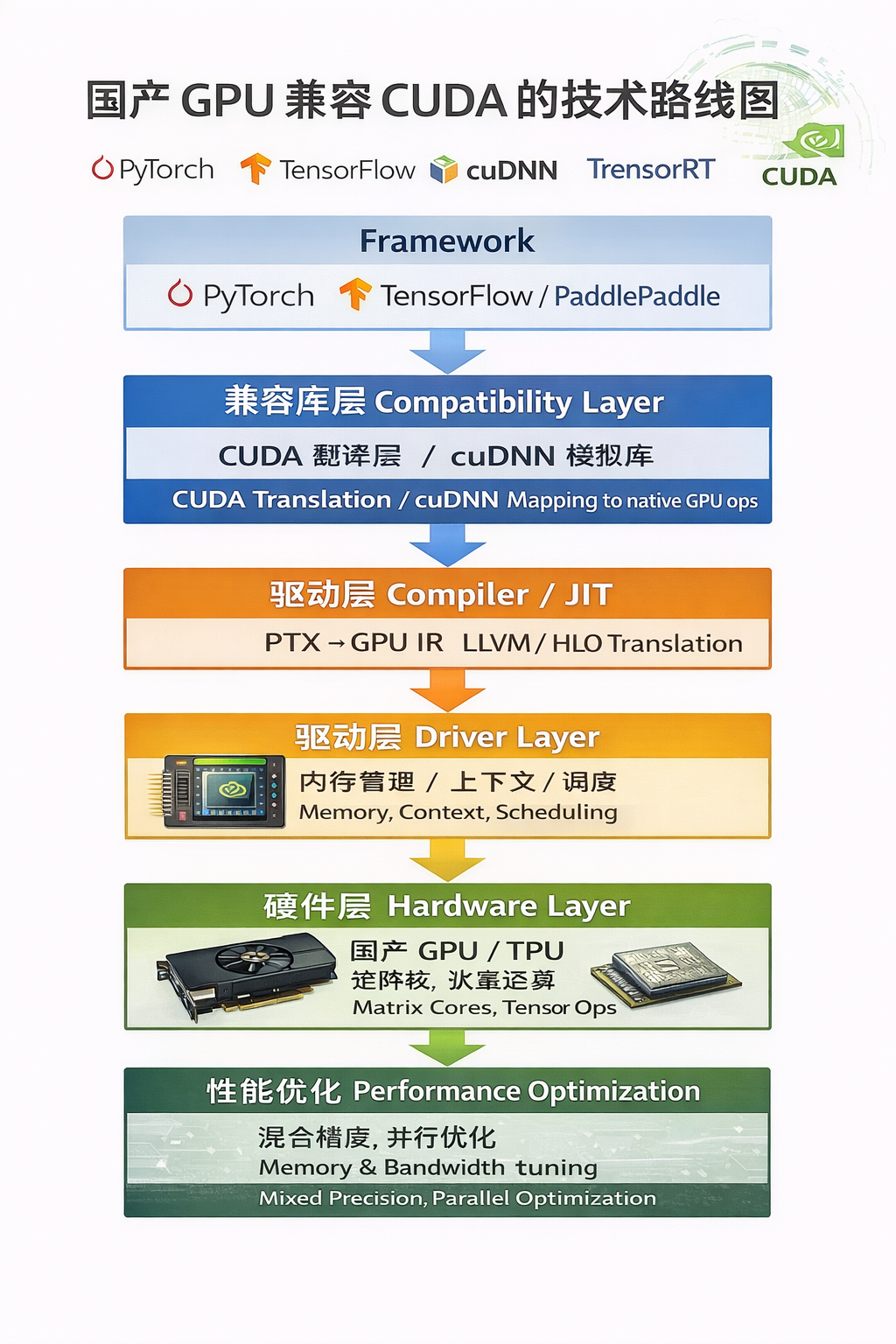
国产 GPU 兼容 CUDA 技术路线图
| 层次 | 技术内容 | 说明 |
|---|---|---|
| Framework 层 | PyTorch / TensorFlow / PaddlePaddle | 支持原生 CUDA 调用 API 的兼容层 |
| 兼容库层 (Middleware) | CUDA 翻译层 / cuDNN 模拟库 | 将 CUDA API 映射到国产 GPU 指令集或算子库 |
| 驱动层 | ROCm 类似驱动 / 自研 GPU 驱动 | 实现 GPU 资源管理、内存分配、上下文切换 |
| 硬件层 | 国产 GPU / TPU | 提供矩阵计算、并行线程调度、带宽优化 |
| 编译器优化 | JIT / LLVM IR / PTX 翻译 | 将 CUDA PTX 或 HLO 代码转换为国产 GPU 可执行指令 |
| 性能优化 | 矩阵核优化、张量并行、混合精度 | 保证运行效率接近 NVIDIA GPU |
0
次点赞