AI

深度学习三

基于Python的理论和实现

Posted by LXG on February 13, 2026

误差反向传播法

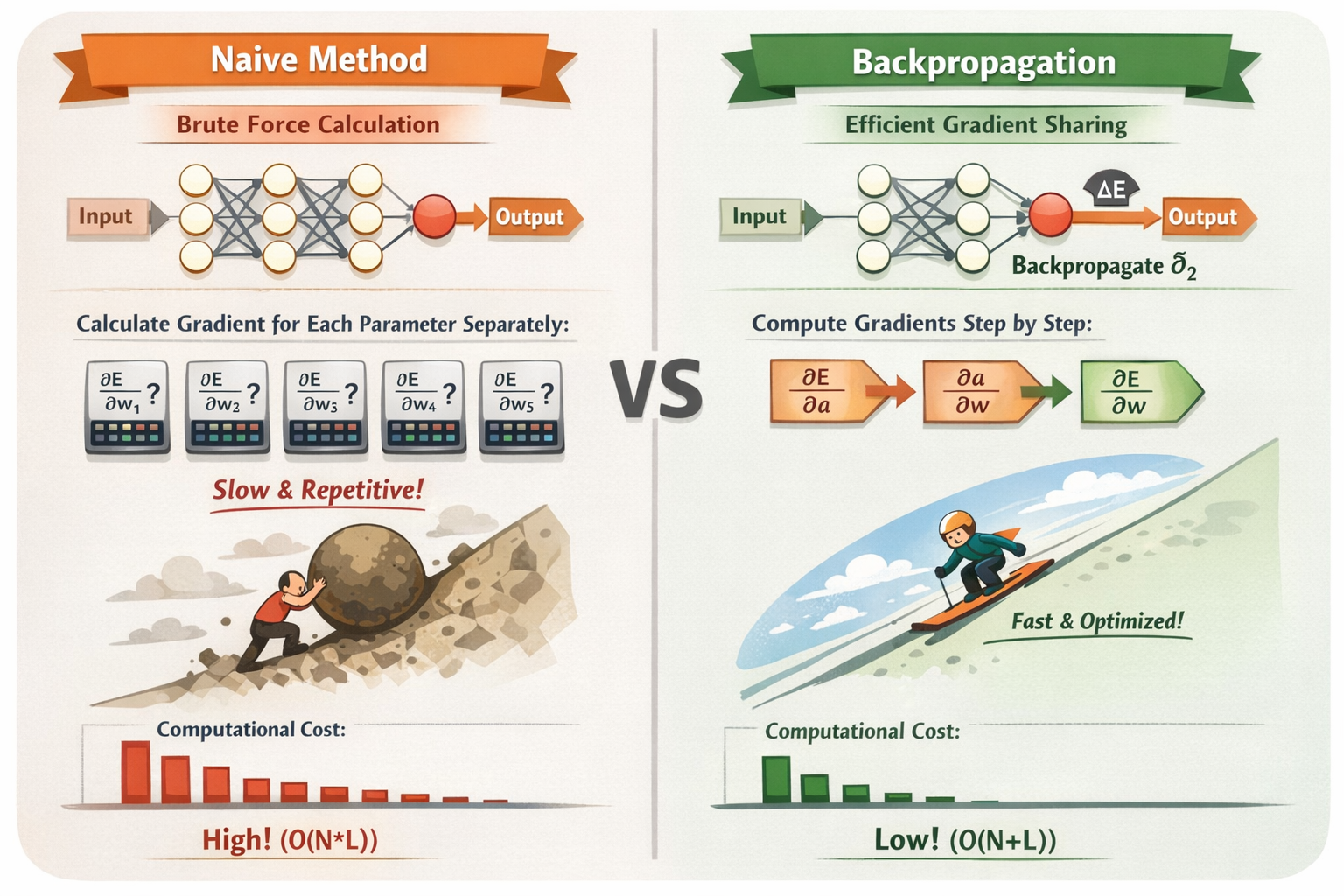
前向传播 + 反向传播对比计算量的示意图

backpropagation

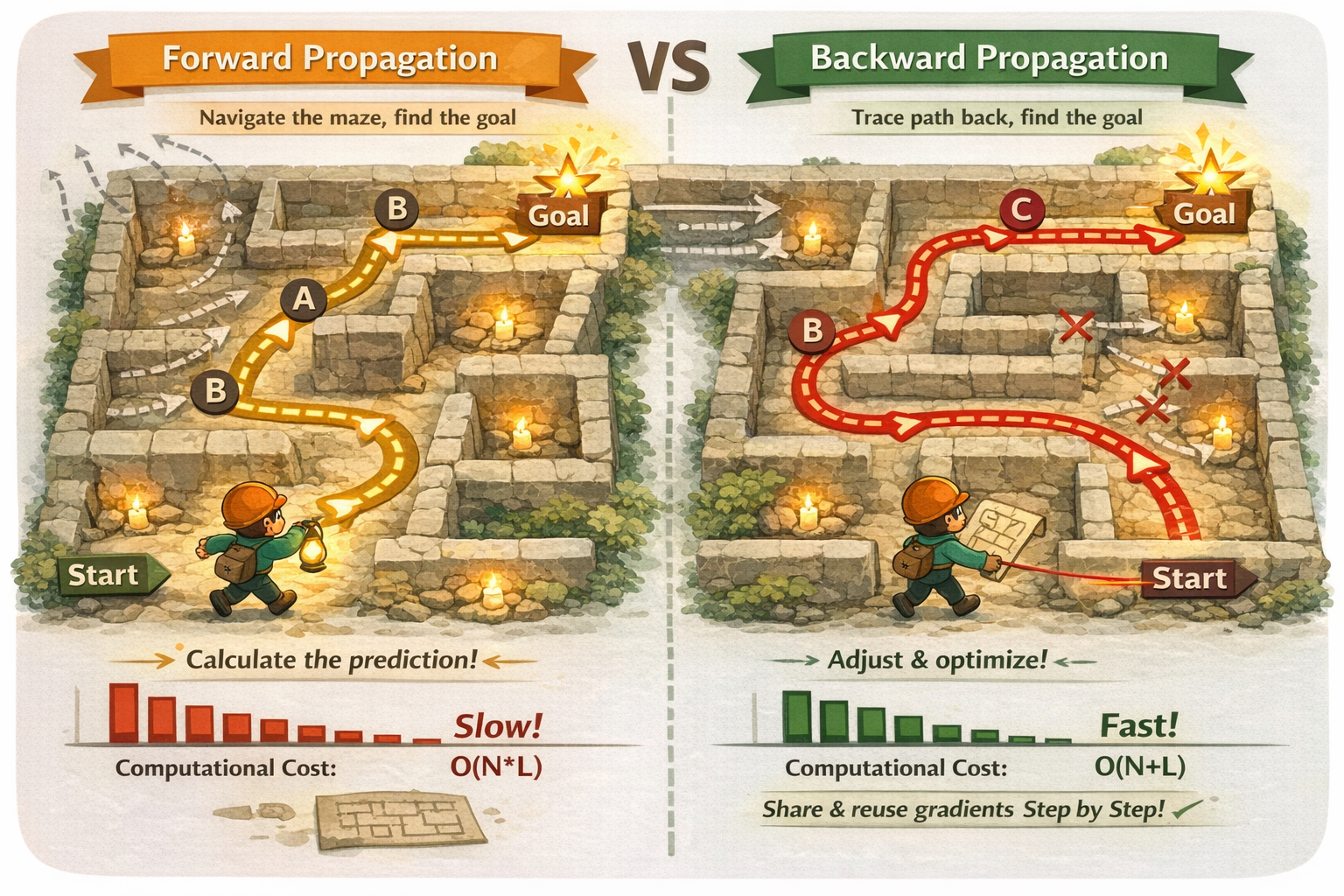
用迷宫来理解反向传播

backpropagation_2

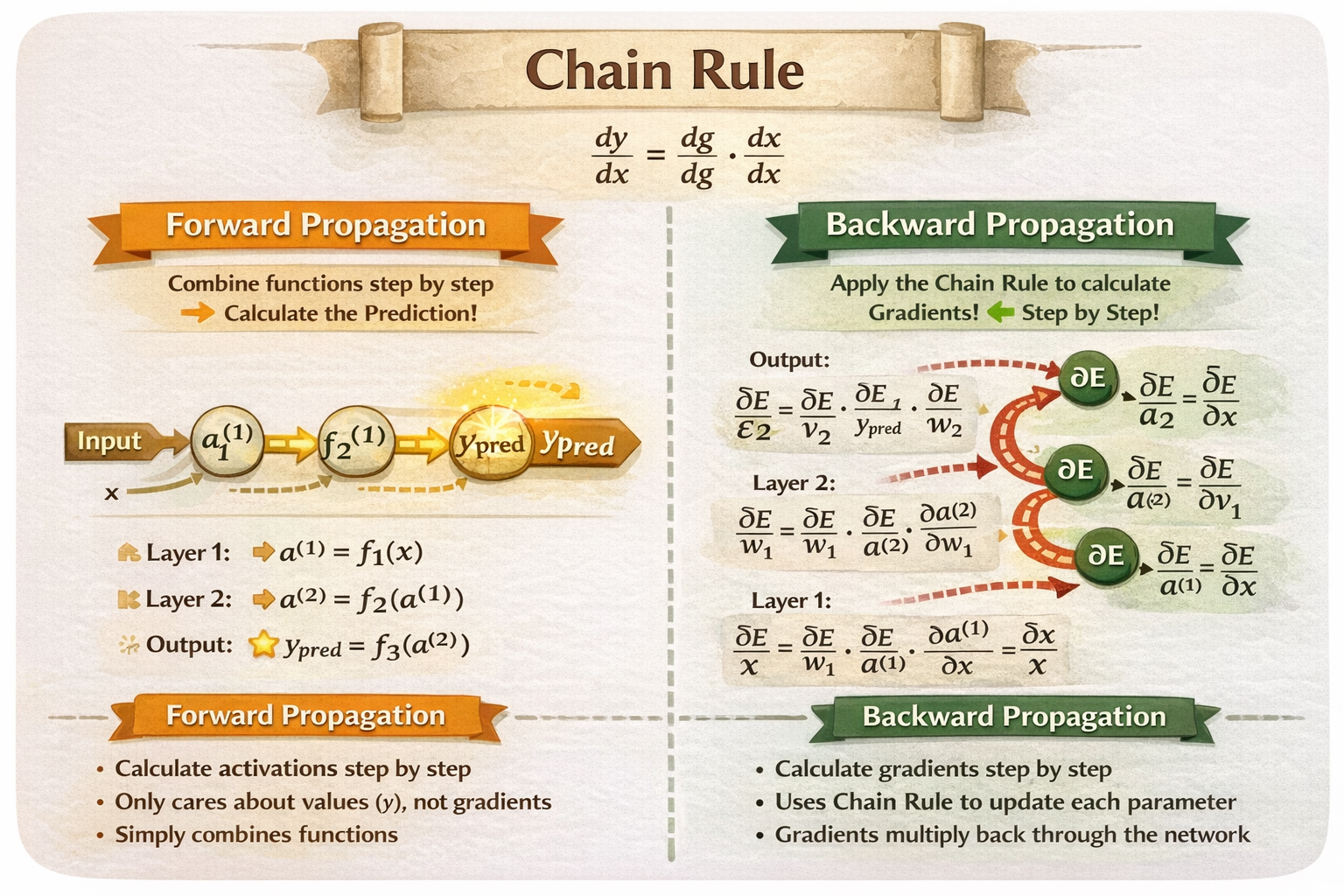
计算图

  • 正向传播(forward propagation) = 预测结果
  • 反向传播(backward propagation) = 分析错误原因，告诉每个神经元怎么调整

链式法则

  • 前向传播中链式法则： 就像流水线上每个工序，把材料一步步加工成半成品 → 最终得到成品。你只关心材料怎么经过每一层，最终变成成品，不关心每个工序对最终误差的贡献。
  • 反向传播中链式法则： 链式法则就像在流水线末端发现问题（成品有瑕疵），你要沿传送带回头追溯每个工序对这个问题的影响，然后告诉每台机器该如何调整。你需要知道每一层“对最终误差的贡献”，才能高效更新参数。

backpropagation_3

比喻

  • 前向传播 = 你每个机器都单独调试一次 → 每次都要重新运行整个流水线
  • 反向传播 = 你先让流水线走一次，把每台机器的中间状态记录下来 → 回溯计算每台机器对最终产品影响 → 不用重复跑整条线

GPU 进入深度学习的时间表

NVIDIA GPU 开始进入深度学习领域

1986年 Rumelhart 等人系统化提出“多层前馈神经网络的误差反向传播训练算法”，并演示它在实际任务中有效，才让反向传播真正成为神经网络训练的核心方法

年份 事件 备注
2006 深度信念网络提出 Hinton 等人，推动深度学习复兴
2007 CUDA 平台发布 NVIDIA 开放 GPU 并行计算能力
2009 深度学习开始用 GPU 训练 Hinton 团队训练 MNIST、ImageNet 子集
2012 AlexNet 获 ImageNet 冠军 使用 NVIDIA GPU 训练 CNN，GPU 成为深度学习训练标准

GPU厂商进入深度学习领域时间对比

厂商 平台 / 技术 进入深度学习应用时间 备注 / 特点
NVIDIA CUDA 2007（平台发布），2009–2010（研究者开始训练深度网络） 第一个成熟并行计算工具，生态完善，GPU训练深度网络主流
AMD Stream SDK / OpenCL 2009–2012 工具和生态不如 CUDA 成熟，少数研究团队尝试训练神经网络
Intel CPU / Xeon Phi / FPGA 2007–2012 以 CPU 为主，Xeon Phi 用于并行计算，FPGA 做实验性加速，GPU通用计算滞后
IBM Cell/Broadband Engine 2008–2011 PS3 GPU/Cell 架构用于小型神经网络实验，实际大规模训练受限
ARM Mali GPU 2010–2013 移动端低功耗 GPU，适合轻量级网络或嵌入式推理，训练能力有限
Google TPU (Tensor Processing Unit) 2016 专用深度学习加速器，面向训练和推理，非通用 GPU，但极大提升大规模训练效率
FPGA 厂商 OpenCL / 自定义加速 2012–2015 用于实验性神经网络加速，灵活但开发复杂，生态不成熟

简单层的实现

apple_demo


class MulLayer:
    """
    乘法层（Multiplication Layer）用于前向传播计算两个输入的乘积
    并在反向传播中计算梯度。
    适用于简单的神经网络或计算图中的乘法节点。
    """
    
    def __init__(self):
        # 初始化时，保存前向传播的输入值
        self.x = None  # 保存输入 x
        self.y = None  # 保存输入 y

    def forward(self, x, y):
        """
        前向传播
        输入: x, y（两个标量或数组）
        输出: x * y（乘积）
        """
        # 保存输入值，用于反向传播计算梯度
        self.x = x
        self.y = y
        # 返回乘积
        return x * y

    def backward(self, dout):
        """
        反向传播
        输入: dout（上一层传递下来的梯度）
        输出: dx, dy（相对于 x 和 y 的梯度）
        
        反向传播公式：
        - 对 x 的梯度 dx = dout * y
        - 对 y 的梯度 dy = dout * x
        """
        # 根据链式法则计算梯度
        dx = dout * self.y  # ∂L/∂x = ∂L/∂out * ∂out/∂x = dout * y
        dy = dout * self.x  # ∂L/∂y = ∂L/∂out * ∂out/∂y = dout * x
        return dx, dy


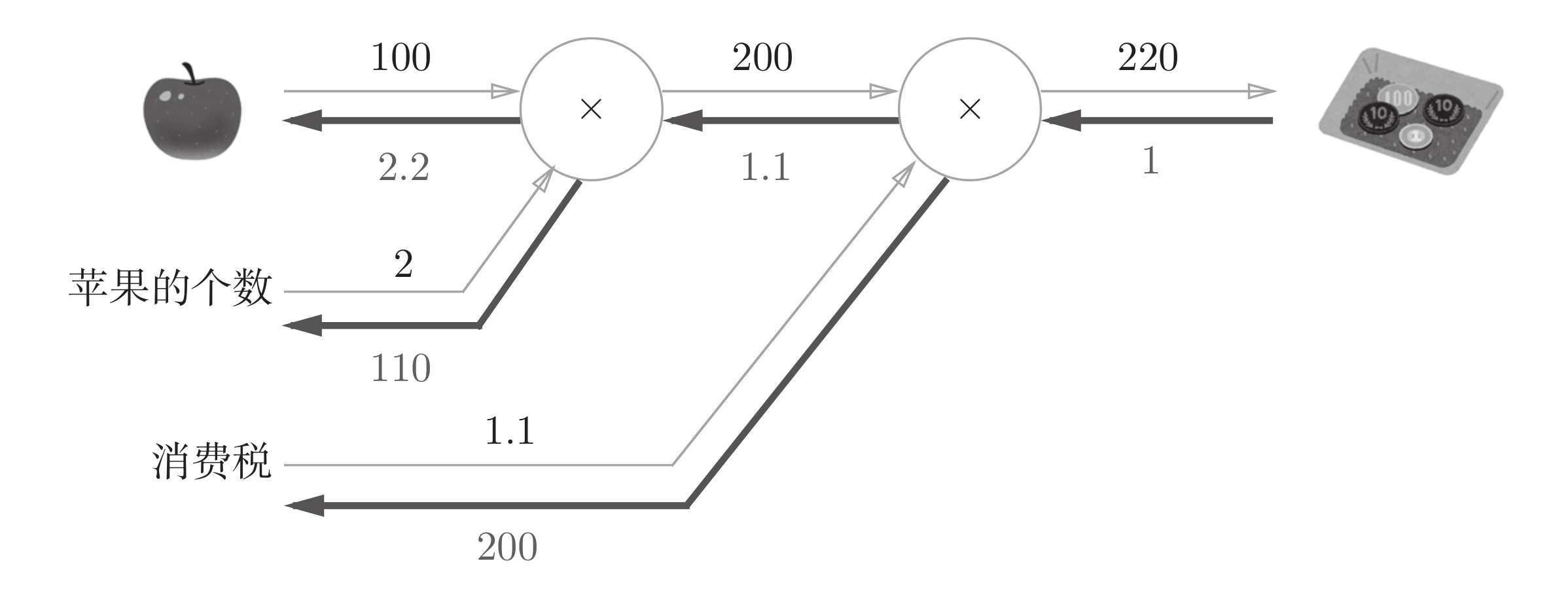
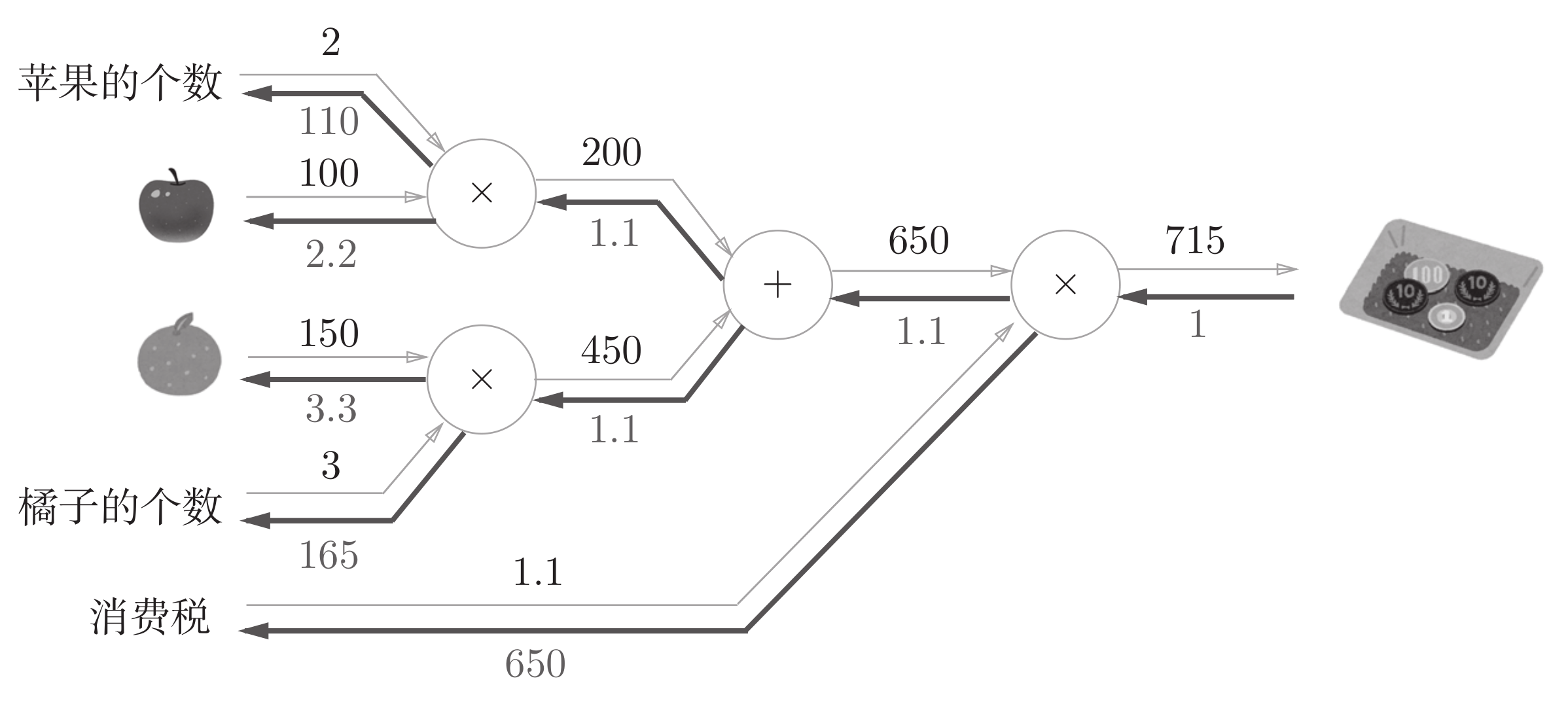
apple_price = 100  # 苹果价格
apple_num = 2      # 苹果数量
tax = 1.1          # 税率

# 创建乘法层实例
mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()

# 前向传播
apple_price = mul_apple_layer.forward(apple_price, apple_num)  # 计算苹果总价
total_price = mul_tax_layer.forward(apple_price, tax)          # 计算含税

print("总价（含税）:", total_price)

# 反向传播
dtotal_price = 1  # 假设总价的梯度为 1
dapple_price, dtax = mul_tax_layer.backward(dtotal_price)  # 计算含税价格对苹果总价和税率的梯度
dapple, dapple_num = mul_apple_layer.backward(dapple_price)  # 计算苹果总价对单价和数量的梯度

print("苹果单价的梯度:", dapple)  # 2.2
print("苹果数量的梯度:", dapple_num) # 110.0

apple_orange_demo


class AddLayer:
    """
    加法层（Addition Layer）用于前向传播计算两个输入的和
    并在反向传播中计算梯度。
    适用于简单的神经网络或计算图中的加法节点。
    """
    
    def __init__(self):
        # 加法层不需要保存输入值，因为梯度是常数1
        pass

    def forward(self, x, y):
        """
        前向传播
        输入: x, y（两个标量或数组）
        输出: x + y（和）
        """
        return x + y

    def backward(self, dout):
        """
        反向传播
        输入: dout（上一层传递下来的梯度）
        输出: dx, dy（相对于 x 和 y 的梯度）
        
        反向传播公式：
        - 对 x 的梯度 dx = dout * 1
        - 对 y 的梯度 dy = dout * 1
        """
        dx = dout * 1  # ∂L/∂x = ∂L/∂out * ∂out/∂x = dout * 1
        dy = dout * 1  # ∂L/∂y = ∂L/∂out * ∂out/∂y = dout * 1
        return dx, dy

apple_price = 100  # 苹果价格
apple_num = 2      # 苹果数量
orange_price = 150 # 橙子价格
orange_num = 3     # 橙子数量
tax = 1.1          # 税率

# 创建乘法层和加法层实例
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()

# 前向传播
apple_total_price = mul_apple_layer.forward(apple_price, apple_num)    # 计算苹果总价
orange_total_price = mul_orange_layer.forward(orange_price, orange_num)  # 计算橙子总价
total_price = add_apple_orange_layer.forward(apple_total_price, orange_total_price)  # 计算总价
total_price_with_tax = mul_tax_layer.forward(total_price, tax)          # 计算含税总价

# 输出总价（含税）
print("总价（含税）:", total_price_with_tax)

# 反向传播
dtotal_price_with_tax = 1  # 假设总价的梯度为 1
dtotal_price, dtax = mul_tax_layer.backward(dtotal_price_with_tax)  # 计算含税总价对总价和税率的梯度
dapple_total_price, dorange_total_price = add_apple_orange_layer.backward(dtotal_price)  # 计算总价对苹果总价和橙子总价的梯度
dapple_price, dapple_num = mul_apple_layer.backward(dapple_total_price)      # 计算苹果总价对单价和数量的梯度
dorange_price, dorange_num = mul_orange_layer.backward(dorange_total_price)  # 计算橙子总价对单价和数量的梯度

# 输出各项的梯度
print("苹果单价的梯度:", dapple_price)        # 2.2
print("苹果数量的梯度:", dapple_num)          # 110.0
print("橙子单价的梯度:", dorange_price)      # 3
print("橙子数量的梯度:", dorange_num)        # 165.0
print("税率的梯度:", dtax)                    # 250.0

ReLU 层 - Rectifired Linear Unit


class Relu:
    """
    ReLU 激活层（Rectified Linear Unit）

    功能：
    前向传播：将输入中小于等于 0 的部分置为 0，大于 0 的部分保持不变
    反向传播：梯度只在输入 > 0 的位置传递，其余位置梯度为 0

    数学形式：
    forward:  out = max(0, x)
    backward: dx = dout (x > 0), 否则为 0
    """

    def __init__(self):
        # mask 用于记录前向传播时哪些位置的输入 <= 0
        # 在反向传播中，这些位置的梯度需要被置为 0
        self.mask = None

    def forward(self, x):
        """
        前向传播

        参数：
        x : 输入数据（可以是标量、向量或矩阵，通常为 numpy 数组）

        过程：
        1. 记录所有 <= 0 的位置（生成布尔数组 mask）
        2. 复制一份输入，避免直接修改原始数据
        3. 将 <= 0 的位置全部置为 0

        返回：
        out : ReLU 处理后的输出
        """
        # 生成布尔掩码，True 表示该位置的值 <= 0
        self.mask = (x <= 0)

        # 复制输入数据，防止直接改动原数据
        out = x.copy()

        # 将 mask 对应位置的值置为 0（即负数和 0 都变为 0）
        out[self.mask] = 0

        return out

    def backward(self, dout):
        """
        反向传播

        参数：
        dout : 上一层传回来的梯度（损失函数对当前层输出的偏导）

        过程：
        根据 ReLU 的导数：
        - 当 x > 0 时，导数为 1，梯度正常传递
        - 当 x <= 0 时，导数为 0，梯度被截断

        因此：
        将前向传播中记录的 mask 位置对应的梯度置为 0

        返回：
        dx : 传递给前一层的梯度
        """

        # 在输入 <= 0 的位置，梯度设为 0
        dout[self.mask] = 0

        # 剩余位置梯度保持不变并继续向前传播
        return dout

ReLU 层的作用就像电路中的开关一样

CATALOG